IDENTITAS TRIGONOMETRI SUDUT RANGKAP
Pengertian Identitas Trigonometri
*Sudut Istimewa
Rumus Sudut Rangkap dibedakan menjadi 3 yaitu:
~ Rumus sudut rangkap Fungsi Sinus
~ Rumus sudut rangkap Fungsi Cosinus
~ Rumus sudut rangkap Fungsi Tangen
1. Rumus sudut rangkap fungsi Sinus
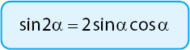
Dari mana fungsi rumus sudut rangkap fungsi sinus di atas diperoleh? Perhatikan pembuktian yang akan diberikan berikut.
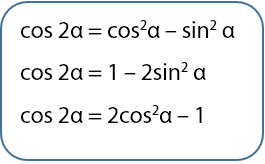
Bukti:
Persamaan pertama:
Persamaan kedua:
Persamaan ketiga:
Terbukti benar untuk tiga persamaan pada sudut rangkap fungsi cosinus
3. Rumus Sudut Rangkap Fungsi Tangen.
Ketiga adalah bahasan rumus sudut rangkap untuk fungsi tangen. Terdapat sebuah persamaan yang menyatakan persamaan sudut rangkap fungsi tangen. Rumus sudut rangkap sinus dinyatakan dalam rumus berikut.
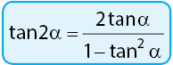
Dari mana persamaan di atas diperoleh? Perhatikan pembuktian berikut.
Bukti:
Terbukti
*Contoh Soal
jika diketahui:
di mana α merupakan sudut lancip, tentukan nilai sin 2 α!
Pembahasan:
Sehingga,

Komentar
Posting Komentar